Shapes of orbitals[edit]

Cross-section of computed hydrogen atom orbital (
ψ(r, θ, φ)2) for the 6s
(n = 6, ℓ = 0, m = 0) orbital. Note that s orbitals, though spherically symmetrical, have radially placed wave-nodes for
n > 1. However, only s orbitals invariably have a center anti-node; the other types never do.
Simple pictures showing orbital shapes are intended to describe the angular forms of regions in space where the electrons occupying the orbital are likely to be found. The diagrams cannot, however, show the entire region where an electron can be found, since according to quantum mechanics there is a non-zero probability of finding the electron (almost) anywhere in space. Instead the diagrams are approximate representations of boundary or
contour surfaces where the probability density
| ψ(r, θ, φ) |2 has a constant value, chosen so that there is a certain probability (for example 90%) of finding the electron within the contour. Although
| ψ |2 as the square of an
absolute value is everywhere non-negative, the sign of the
wave function ψ(r, θ, φ) is often indicated in each subregion of the orbital picture.
Sometimes the ψ function will be graphed to show its phases, rather than the | ψ(r, θ, φ) |2 which shows probability density but has no phases (which have been lost in the process of taking the absolute value, since ψ(r, θ, φ) is a complex number). | ψ(r, θ, φ) |2 orbital graphs tend to have less spherical, thinner lobes thanψ(r, θ, φ) graphs, but have the same number of lobes in the same places, and otherwise are recognizable. This article, in order to show wave function phases, shows mostly ψ(r, θ, φ) graphs.
The lobes can be viewed as
interference patterns between the two counter rotating "
m" and "
−m" modes, with the projection of the orbital onto the xy plane having a resonant "
m" wavelengths around the circumference. For each
m there are two of these
⟨m⟩+⟨−m⟩ and
⟨m⟩−⟨−m⟩. For the case where
m = 0 the orbital is vertical, counter rotating information is unknown, and the orbital is z-axis symmetric. For the case where
ℓ = 0 there are no counter rotating modes. There are only radial modes and the shape is spherically symmetric. For any given
n, the smaller
ℓ is, the more radial nodes there are. Loosely speaking
n is energy,
ℓ is analogous to
eccentricity, and
m is orientation.
Generally speaking, the number n determines the size and energy of the orbital for a given nucleus: as n increases, the size of the orbital increases. However, in comparing different elements, the higher nuclear charge Z of heavier elements causes their orbitals to contract by comparison to lighter ones, so that the overall size of the whole atom remains very roughly constant, even as the number of electrons in heavier elements (higher Z) increases.
Also in general terms,
ℓ determines an orbital's shape, and
mℓ its orientation. However, since some orbitals are described by equations in
complex numbers, the shape sometimes depends on
mℓ also. Together, the the whole set of orbitals for a given
ℓ and
n fill space as symmetrically as possible, though with increasingly complex sets of lobes and nodes.
The single s-orbitals (
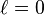
) are shaped like spheres. For
n = 1 it is roughly a
solid ball (it is most dense at the center and fades exponentially outwardly), but for
n = 2 or more, each single s-orbital is composed of spherically symmetric surfaces which are nested shells (i.e., the "wave-structure" is radial, following a sinusoidal radial component as well). See illustration of a cross-section of these nested shells, at right. The s-orbitals for all
n numbers are the only orbitals with an anti-node (a region of high wave function density) at the center of the nucleus. All other orbitals (p, d, f, etc.) have angular momentum, and thus avoid the nucleus (having a wave node
at the nucleus).
The three p-orbitals for
n = 2 have the form of two
ellipsoids with a
point of tangency at the
nucleus (the two-lobed shape is sometimes referred to as a "
dumbbell"—there are two lobes pointing in opposite directions from each other). The three p-orbitals in each
shell are oriented at right angles to each other, as determined by their respective linear combination of values of
mℓ. The overall result is a lobe pointing along each direction of the primary axes.

The five d orbitals in
ψ(x, y, z)2 form, with a combination diagram showing how they fit together to fill space around an atomic nucleus.
Four of the five d-orbitals for
n = 3 look similar, each with four pear-shaped lobes, each lobe tangent at right angles to two others, and the centers of all four lying in one plane. Three of these planes are the xy-, xz-, and yz-planes—the lobes are between the pairs of primary axes—and the fourth has the centres along the on the x and y axes themselves. The fifth and final d-orbital consists of three regions of high probability density: a
torus with two pear-shaped regions placed symmetrically on its z axis. The overall total of 18 directional lobes point in every primaxy axis direction and between every pair.
There are seven f-orbitals, each with shapes more complex than those of the d-orbitals.
Additionally, as is the case with the s orbitals, individual p, d, f and g orbitals with n values higher than the lowest possible value, exhibit an additional radial node structure which is reminiscent of harmonic waves of the same type, as compared with the lowest (or fundamental) mode of the wave. As with s orbitals, this phenomenon provides p, d, f, and g orbitals at the next higher possible value of n (for example, 3p orbitals vs. the fundamental 2p), an additional node in each lobe. Still higher values of n further increase the number of radial nodes, for each type of orbital.
The shapes of atomic orbitals in one-electron atom are related to 3-dimensional
spherical harmonics. These shapes are not unique, and any linear combination is valid, like a transformation to
cubic harmonics, in fact it is possible to generate sets where all the d's are the same shape, just like the
px, py, and
pz are the same shape.
[22][23]
Orbitals table[edit]
This table shows all orbital configurations for the real hydrogen-like wave functions up to 7s, and therefore covers the simple electronic configuration for all elements in the periodic table up to
radium. "ψ" graphs are shown with
− and
+ wave function phases shown in two different colors (arbitrarily red and blue). The
pz orbital is the same as the
p0 orbital, but the
px and
py are formed by taking linear combinations of the
p+1 and
p−1 orbitals (which is why they are listed under the
m = ±1 label). Also, the
p+1 and
p−1 are not the same shape as the
p0, since they are pure
spherical harmonics.
| s (ℓ = 0) | p (ℓ = 1) | d (ℓ = 2) | f (ℓ = 3) |
|---|
| m = 0 | m = 0 | m = ±1 | m = 0 | m = ±1 | m = ±2 | m = 0 | m = ±1 | m = ±2 | m = ±3 |
|---|
| s | pz | px | py | dz2 | dxz | dyz | dxy | dx2−y2 | fz3 | fxz2 | fyz2 | fxyz | fz(x2−y2) | fx(x2−3y2) | fy(3x2−y2) |
|---|
| n = 1 |  | | | | | | | | | | | | | | | |
|---|
| n = 2 |  |  |  |  | | | | | | | | | | | | |
|---|
| n = 3 |  |  |  |  |  |  |  |  |  | | | | | | | |
|---|
| n = 4 |  |  |  |  | 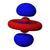 |  |  |  |  |  |  |  |  |  |  |  |
|---|
| n = 5 |  |  |  |  |  |  |  |  |  | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
|---|
| n = 6 |  |  |  |  | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
|---|
| n = 7 |  | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
|---|
Qualitative understanding of shapes[edit]
The shapes of atomic orbitals can be understood qualitatively by considering the analogous case of
standing waves on a circular drum.
[24] To see the analogy, the mean vibrational displacement of each bit of drum membrane from the equilibrium point over many cycles (a measure of average drum membrane velocity and momentum at that point) must be considered relative to that point's distance from the center of the drum head. If this displacement is taken as being analogous to the probability of finding an electron at a given distance from the nucleus, then it will be seen that the many modes of the vibrating disk form patterns that trace the various shapes of atomic orbitals. The basic reason for this correspondence lies in the fact that the distribution of kinetic energy and momentum in a matter-wave is predictive of where the particle associated with the wave will be. That is, the probability of finding an electron at a given place is also a function of the electron's average momentum at that point, since high electron momentum at a given position tends to "localize" the electron in that position, via the properties of electron wave-packets (see the
Heisenberg uncertainty principle for details of the mechanism).
This relationship means that certain key features can be observed in both drum membrane modes and atomic orbitals. For example, in all of the modes analogous to
s orbitals (the top row in the animated illustration below), it can be seen that the very center of the drum membrane vibrates most strongly, corresponding to the
antinode in all
s orbitals in an atom. This antinode means the electron is most likely to be at the physical position of the nucleus (which it passes straight through without scattering or striking it), since it is moving (on average) most rapidly at that point, giving it maximal momentum.
A mental "planetary orbit" picture closest to the behavior of electrons in
s orbitals, all of which have no angular momentum, might perhaps be that of a
Keplerian orbit with the
orbital eccentricity of 1 but a finite major axis, not physically possible (because
particles were to collide), but can be imagined as a
limit of orbits with equal major axes but increasing eccentricity.
Below, a number of drum membrane vibration modes are shown. The analogous wave functions of the hydrogen atom are indicated. A correspondence can be considered where the wave functions of a vibrating drum head are for a two-coordinate system ψ(r, θ) and the wave functions for a vibrating sphere are three-coordinate ψ(r, θ, φ).
s-type modes
Mode
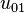
(1s orbital)
Mode

(2s orbital)
Mode

(3s orbital)
None of the other sets of modes in a drum membrane have a central antinode, and in all of them the center of the drum does not move. These correspond to a node at the nucleus for all non-s orbitals in an atom. These orbitals all have some angular momentum, and in the planetary model, they correspond to particles in orbit with eccentricity less than 1.0, so that they do not pass straight through the center of the primary body, but keep somewhat away from it.
In addition, the drum modes analogous to p and d modes in an atom show spatial irregularity along the different radial directions from the center of the drum, whereas all of the modes analogous to s modes are perfectly symmetrical in radial direction. The non radial-symmetry properties of non-s orbitals are necessary to localize a particle with angular momentum and a wave nature in an orbital where it must tend to stay away from the central attraction force, since any particle localized at the point of central attraction could have no angular momentum. For these modes, waves in the drum head tend to avoid the central point. Such features again emphasize that the shapes of atomic orbitals are a direct consequence of the wave nature of electrons.
p-type modes
Mode
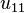
(2p orbital)
Mode

(3p orbital)
Mode
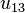
(4p orbital)
d-type modes
Mode

(3d orbital)
Mode

(4d orbital)
Mode

(5d orbital)

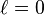 ) are shaped like spheres. For
) are shaped like spheres. For 













































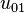 (1s orbital)
(1s orbital)
 (2s orbital)
(2s orbital)
 (3s orbital)
(3s orbital)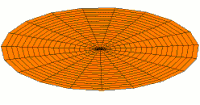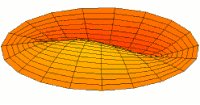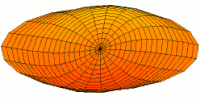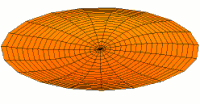
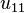 (2p orbital)
(2p orbital)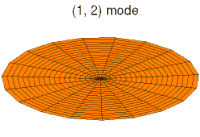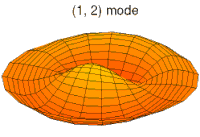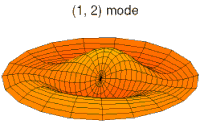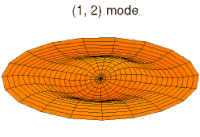
 (3p orbital)
(3p orbital)
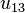 (4p orbital)
(4p orbital)
 (3d orbital)
(3d orbital)
 (4d orbital)
(4d orbital)
 (5d orbital)
(5d orbital)